이산수학 10강을 보며 배운내용
정리(TL;DR)
평면 그래프
모든 변이 교차하지 않는 그래프
오일러 사이클
모든 변을 한 번만 지나고, 시작점과 종점이 같다
해밀턴 사이클
모든 꼭지점을 한 번만 지나고, 시작점과 종점이 같다
가중 그래프
각 변에 가중치가 있는 그래프
최단 경로, 신장 트리 등에 이용
평면 그래프
그래프의 모든 변이 교차하지 않는 그래프
평면 그래프 예시 1
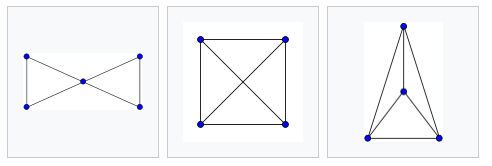
평면 그래프 예시 2
왼쪽의 이미지의 변을 옮기면 오른쪽처럼 되는데 겹치는 변이 없어서 평면 그래프다

오일러의 공식(Euler's Formula)
연결된 평면 그래프에서,
꼭지점의 수 v, 변의 수 e, 면의 수 f 라고 하면
v(꼭지점) - e(변의 수) + f(면의 수) = 2
4색 정리
지도의 인접한 구역을 서로 다른 색으로 칠하려면 4가지 색이면 가능하다
오일러 투어(Eulerian Tour)
시작점과 종점이 같은 오일러 트레일을 오일러 투어라고 한다
닫힌 오일러 투어
오일러 트레일(Eulerian Trail)
그래프의 모든 변을 각각 한 번만 지나는 트레일
투어
그래프의 모든 변들이 포함된 닫힌 워크
오일러 그래프
오일러 투어를 갖는 그래프
오일러 투어와 꼭지점 차수의 짝수는 필요충분 조건
연결 그래프가 오일러 투어를 갖는다면,
그래프의 모든 꼭지점의 차수가 짝수
반대로,
그래프의 모든 꼭지점의 차수가 짝수면,
연결 그래프가 오일러 투어를 갖는다
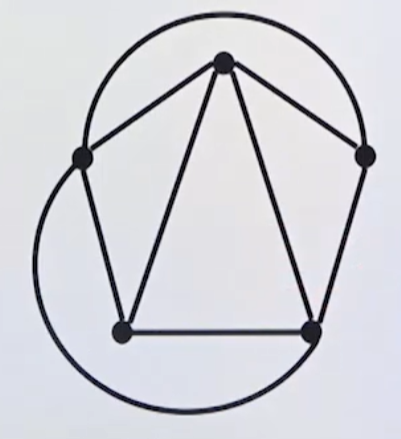
해밀턴 경로(Hamilton Path)
그래프의 모든 꼭지점을 한 번만 지나는 경로
해밀턴 경로 예시

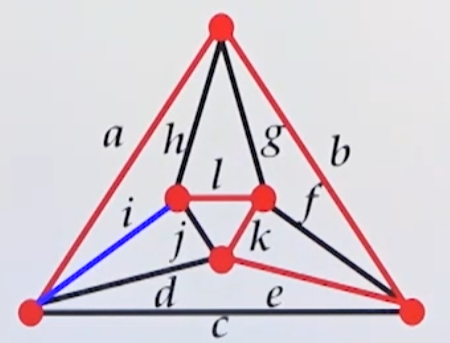
해밀턴 사이클
시작과 종점이 같은 해밀턴 경로
닫힌 해밀턴 경로
해밀턴 사이클 예시
가중 그래프(Weighted Graph)
각 변에 실수값이 붙여진 그래프
이 실수값을 가중치라고 부른다
가중 그래프를 어디에 사용하나?
=> 가중치가 가장 작게 만든다
- 최단 경로 문제
출발지와 도착지가 있을 때 가장 짧은 경로 - 최소 신장 트리 문제
그래프의 모든 꼭지점을 최소 수의 변으로 연결
(다음 강에서 알아보자!)
최단 경로 문제
Dijkstra(다익스트라) 알고리즘 이용
전에 알아본 다익스트라 알고리즘 포스트
알고리즘 8강 :: 욕심쟁이, 최단경로, 작업스케쥴, 작업 선택
알고리즘 8강을 보며 배운내용 들어가기 전 7강 욕심쟁이 방법 강의를 듣고 욕심쟁이 알고리즘 문제를 풀었는데 강의를 들을 때처럼 꽤 직관적으로 해결됐다 포인트는 1. 최솟값 or 최댓값 합이
forgottenknowledge.tistory.com

'Computer Science > Discrete Mathematics :: 이산수학' 카테고리의 다른 글
| 이산수학 12강 :: 순열, 조합, 비둘기집의 원리 (0) | 2022.05.10 |
|---|---|
| 이산수학 11강 :: 트리, 이진트리, 완전이진트리, 이진탐색트리, 최소신장트리 (0) | 2022.05.03 |
| 이산수학 9강 :: 그래프(1/2), 용어, 종류 (0) | 2022.04.21 |
| 이산수학 8강 :: 디지털 논리회로, 부울대수, 부울대수 간소화 (0) | 2022.04.19 |
| 이산수학 7강 :: 함수, 전단사함수, 역함수 (0) | 2022.04.15 |