선형대수 10화를 듣고 배운내용
선형변환(Linear Transformation)
map / mapping / function
T(A + B) = T(A) + T(B)
T(kA) = kT(A)
선형변환이 보존하는 것
- 덧셈을 보존시키고
- 스칼라 배를 보존하는 것이 선현변환
- 영벡터, 역원(음벡터), 뺄셈
- 일차겹합
- 부분공간
- 일차독립
- L(V, W)는 벡터공간 => 선형변환은 다른말로 벡터
=> T는 벡터공간의 성질을 보존시킨다.
주어진 선형변환에 핵과 상을 구할 수 있고, 차원을 구할 수 있으면 성공
전사, 단사, 전단사
전사: 전체 크기일 때, T(V) = Im(T) = W
단사: 부분 크기일 때

사상 T에 대응하는 행렬
T에 대응하는 행렬, T의 행렬이라고 부른다
행렬사상 or 행렬변환

선형변환 다시 살펴보자
두 개의 연산을 보존하는 사상
일차결합도 보존

선형변환이라면
- 원점을 보존해줘야 한다.
- 역원도 보존해줘야 한다.
- 뺄셈도 보존

T가 선형변형이라는 것과 필요충분 조건은

선형변환의 합성

따름정리

일차겹합의 보존

기저의 상(T)으로 선형변환 결정
유일하게 존재

기저 A의 dimension(dim A)은 n차
부분공간의 보존
부분공간도 보존해준다

일차독립성의 보존(역방향)
일차독립도 보존이 된다
역방향 일차독립

선형변환의 상과 핵
부분공간의 보존
핵(Kernel)
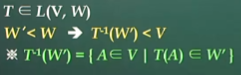
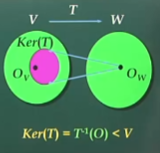

일차독립성의 보존(순방향)
순방향 일차독립


차원공식
참고: '기저'라는것은 일차독립하는 원소들을 모아놓은것
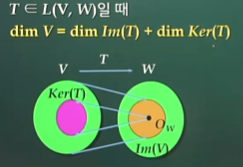
T가 단사 그리고 Ker(T)가 항등원이라는 것에 대한 필요충분조건

따름정리

동현변환, 동형공간
선형변환이 전단사일 때를 동형변환(isomorphism)
V와 W를 동형(isomorphic)이라고 한다.

연습문제

'Computer Science > Linear Algebra :: 선형대수' 카테고리의 다른 글
| 선형대수 강의 12화 :: 고유값, 고유벡터, 특성방정식 (0) | 2021.10.22 |
|---|---|
| 선형대수 강의 11화 :: 선형변환의 행렬 표현, 기저변환행렬 (0) | 2021.10.21 |
| 선형대수 강의 9화 :: 일차 결합, 일차 독립성, 벡터의 기저와 차원 (0) | 2021.10.14 |
| 선형대수 강의 8화 :: 체, 벡터공간, 부분공간 (0) | 2021.10.10 |
| 선형대수 강의 7화 :: 벡터, 벡터 거리, 벡터의 내적 (0) | 2021.09.24 |