이산수학 실시간 강의!
2강 논리
명제(Proposition)란?
참과 거짓을 구별할 수 있는 문장이나 수식
예시) 메시는 호날두보다 발롱도르를 많이 탔다
명제의 진리값을 구하란 말은
명제의 참과 거짓을 붙여주는것
참(True) | 거짓(False)
식이란?
상수와 변수를 연산자로 묶은 것
합성명제
하나 이상의 명제와 논리연산자 그리고 괄호로 이루어진 명제
논리연산자
논리곱, 논리합, 부정, 베타적논리합
1. 논리곱(conjunction)
and 연산
부호: ∧
2. 논리합(disjunction)
or 연산
부호: ∨
3. 부정(negation)
not 연산
부호: ~
4. 베타적 논리합(exclusive or)
or은
p가 참, q가 참이면, 결과도 참인데
xor은
p가 참, q가 참이면, 결과는 거짓이다
즉, 다를 때만 T
같으면 F
논리적 동치 법칙을 살펴보자
외우지 않아도 이해를 하면 될 듯 싶다
- 교환법칙
- 겹합법칙
- 분대법칙
- 항등법칙
- 지배법칙
- 부정법칙
- 멱등법칙
- 드 모르간 법칙
- 흡수법칙
- 함축법칙
- 대우법칙
- ... 등
항진명제
항상 참인 명제
모순명제
항상 거짓인 명제
인공지능시 필요한 수학은 이렇게 3개라고 한다
선형대수(중요), 편미분학, 확률
6강 관계
곱집합(Cartesian Product)
집합 A, B의 곱집합 A x B는
A의 원소와 B의 원소의 모든 순서쌍(ordered pair)들의 집합
관계(relation)
집합 X에서 집합 Y로의 관계 R은
곱집합 X x Y의 부분집합
XY ∈ R
X = Y면 R을 X에서의 관계
관계의 표현
1. 화살표 도표
2. 방향 그래프
방향그래프로 나타내는 법
- 정점 A의 정점을 좌표로 표시
- T를 화살표를 그려준다

3. 부울행렬
행렬이 모든 원소가 부울값으로만 구성된 행렬
부울값(boolean matrix)
0 아니면 1
부울행렬로 나타내는 법
- A x A에서
- T의 좌표를 1, 나머지는 0 적어주면 된다

관계의 성질
집합 A에서의 관계 R
1. 반사적(reflexive)
A의 어떤 원소를 꺼내도 R에 속하면 반사적
2. 대칭적(symmetric)
A에서 아무 원소나 꺼내서
(a, b) ∈ R 이고 (b, a) ∈ R이면 대칭적이라 한다
3. 추이적(transitive)
A에서 세 원소를 꺼내서
이 세가지 만족하면 동치관계

- 반사적 구분법
모든 정점에 self-loop 있어야된다 - 대칭적 구분법
가는 선, 오는 선 같이 있어야한다 - 추이적 구분법
a에서 b로 가고, b에서 c로간다면 a, c로도 가야된다


7강 함수
정의역
입력값
보통 X로 표현
치역
출력값
Y
함수의 종류
- 전사함수(Surjective Function)
정의역과 치역이 완전히 같을 때
- 단사함수(Injective Function)
x1 != x2 이렇게 다르면
y1 != y2 이러면 단사
일대일로 대응해야지 단사함수
같은 치역을 가지면 단사함수가 아니다
- 전단사함수(Bijective Function)
전사이면서 단사 함수
- 역함수(Inverse Function)
역함수가 있으려면 전단사함수여야 한다
- 합성함수(Composition Function)
함수 중복한 것
(g ∘ f )(x) 이렇게 나타내기로 약속
- 계승함수(Factorial Function)
팩토리얼 잘 정리된 링크
=> 나무위키 계승
- 바닥함수(Floor Function)
실수를 정수로 바꿀 때 바닥값 이용
갑자기 떠오른 Math.floor
- 천장함수(Ceiling Function)
실수를 정수로 만들 때 천장값 이용
Math.ceil 이겠지
- 나머지 함수(Modulo Function)
나머지 구하는 함수
n을 m으로 나눴을 때 나머지 => n mod m
나머지 함수 음수
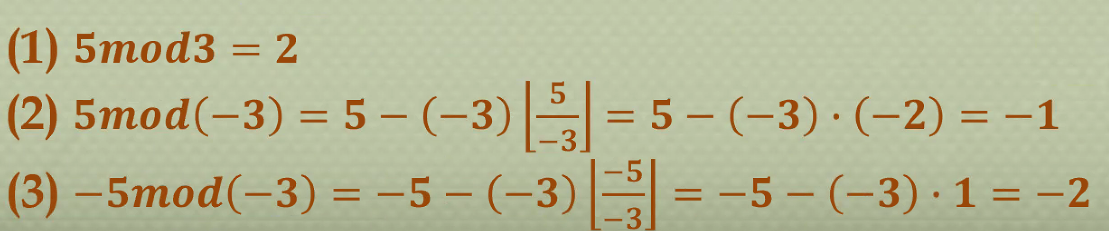
- 해시(hash) 함수
큰 정수집합에서 작은 정수로 만들 때 주로 나머지 함수 이용

'Computer Science > Discrete Mathematics :: 이산수학' 카테고리의 다른 글
| 이산수학 5강 :: 행렬, 기본연산, 10가지 행렬의 종류 (0) | 2022.04.01 |
|---|---|
| 이산수학 4강 :: 집합, 집합연산, 대수법칙 (0) | 2022.03.29 |
| 이산수학 3강 :: 공리, 증명, 정리, 증명법 (0) | 2022.03.26 |
| 이산수학 2강 :: 명제, 논리연산, 술어논리 (0) | 2022.03.15 |
| 이산수학 1강 :: 이산수학, 자료구조 (0) | 2022.03.08 |