그래프
정점: 여러가지 특성을 가지는 객체
간선: 정점들 간의 관계
그래프 종류
무방향그래프: 정점간 방향이 없는 그래프
방향 그래프: 정점간 방향이 있는 그래프
그래프 특징
자기 자신을 향하는 간선은 없다
중복된 간선은 없다
그래프 표현 방식
인접행렬 - 무방향 그래프
대각선 기준으로 대칭이다
가중치 없을 때 0, 1로 표현

인접행렬 - 무방향 그래프 feat. 가중치
가중치 있어서 가중치

인접행렬 - 방향 그래프

인접행렬 - 방향 그래프 feat 가중치

# 그래프 표시
# Dictionary
graph = {0: {1: 5, 2: 1, 3: 1}, 2: {1: 4}, 3: {0: 3}}
# List
graph = [[0, 5, 1, 1], [0, 0, 0, 0], [0, 4, 0, 0], [3, 0, 0, 0]]
인접리스트 - 무방향 그래프
중간의 화살표는 뒤에 것을 가리키고 있다는 말이 아니다
예시)
✔️ header 0이 1(가중치 2), 2(가중치 3), 3(가중치 8)을 가지고 있는 것이고
❌ header 0 줄에 1(가중치 2)가 2(가중치 3)을 가리키고 있는게 아니다
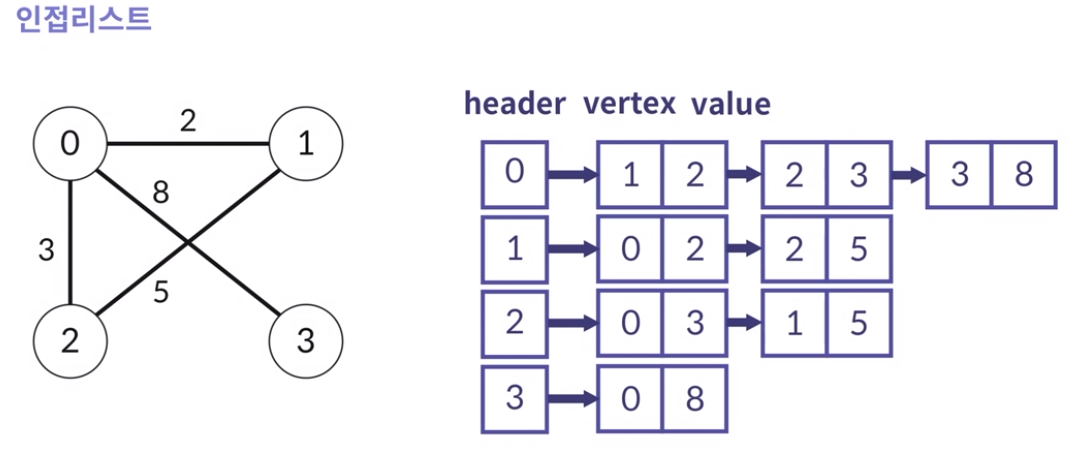
인접리스트 - 방향 그래프
1은 어디로 나가는 간선이 없어서 ZERO

// 인접리스트 그래프 표현
class AdjNode:
def __init__(self, vertex, value):
self.vertex = vertex
self.value = value
self.next = None
그래프 탐색 방법 BFS | DFS
너비우선탐색(BFS: Breadth First Search)
부모 공유하는 인접노드 우선 탐색
깊이 우선 탐색(DFS: Depth First Search)
해당 분기 다 탐색하고 넘어가는 탐색법
모든 지점 확인할 때는 DFS, BFS 어떤 것도 상관없다
한 지점 여러 번 들리지 않으니까, 같은 시간 복잡도를 갖는다
언제 BFS 사용할까?
BFS는 가까운 순서대로 방문한다
한 지점으로 가는 최단 경로는 BFS를 사용한다
거리가 짧은 순서대로 방문하기 때문에,
BFS 통해 목적지 처음 방문했다면 그 거리가 최단거리다
=> Queue와 좌표로 거리를 알 수 없어서 별도로 거리 정보 저장해야된다.
Queue 사용 BFS 예시
# 너비우선탐색(Breadth First Search)
def BFS (graph, root):
visited = set([root])
search = []
queue = deque([root])
while queue:
cur == queue.popleft()
search.append(cur)
for node in graph[cur]:
if node not in visited:
queue.append(node)
visited.add(node)
return search
언제 DFS 사용할까?
다양한 경로는 DFS 사용한다
DFS는 한 지점을 여러번 방문하지만 전체 경로는 중복되지 않도록 경로를 확인 가능하다
=> 재귀함수, 스택, 좌표로 경고를 모르니까, 경로 정보를 저장해줘야 한다
Stack 사용 예시
# 스택이용 DFS 구현
def DFS(graph, start_node):
visit = [start_node]
stack = []
stack.append(start_node)
cur = start_node
while stack:
for node in graph[cur];
if node not in visited;
stack.append(node)
visited.append(node)
cur = node
break
else:
stack.pop()
if stack : cur = stack[-1]
return visited
재귀함수 예시
# 재귀이용 DFS
def DFS (graph, cur) :
global visited
if cur not in visited:
visited.append(cur)
for node in graph[cur]:
DFS(graph, node)

'Computer Science > Algorithm :: 알고리즘' 카테고리의 다른 글
| 알고리즘 2강 :: 대표적인 알고리즘 3가지, 점근 성능 (0) | 2022.02.24 |
|---|---|
| 알고리즘 1강 :: 모든 자료구조 구현은 배열과 연결리스트 (0) | 2022.02.22 |
| 알고리즘 :: 재귀호출, 수학적 귀납법, 퀵정렬, 재귀함수 디자인 (0) | 2021.12.20 |
| 알고리즘 :: JavaScript 여러 줄 입력 받는 법 (1) | 2021.11.10 |
| 알고리즘 :: 구름 - Binary Search #JavaScript (0) | 2021.10.01 |