알고리즘 3강을 보며 배운내용
3대 알고리즘중 하나 분할정복 방법의 원리, 특징, 단계를 알아봐야지
분할정복 방법 원리
순환적(recursively) 문제를 하향식(top-down) 접근
문제를 계속 분할하고,
해결된 값(해)를 결합해서 문제의 답을 구한다
특징
분학된 작은 문제는 원래 문제와 같다
입력 크키가 작아진 것
분할된 작은 문제는 독립적이다
그래서 반복해서 분할과 결과를 합칠 수 있다
처리 단계
분할: 문제를 여러 개의 작은 문제로 나누기
정복: 작은 문제를 더 분할되지 않을 크기가 되면 해를 구하기
결합: 정복된 해를 결합해서 원래 문제의 해(값)을 구한다
결합 단계가 없는 문제도 있다고 한다
분할 정복은 어디에 쓸까?
이진 탐색, 퀵 정렬, 합병 정렬, 선택 문제
- 이진 탐색
한 쪽만 조지는 방법
절반 쪼개고, 그 중 한쪽만 또 쪼개고, 또 쪼개고 또 쪼개고 ...
- 합병 정렬
공평하게 사용
전체적으로 반반씩 쪼개고 쪼개고
- 퀵 정렬
불공평하게 나눈다
딱 반으로 안쪼갠다
- 선택 문제
얘도 불공평하게 나누는데
이진 탐색처럼 한쪽만 집중한다
이진 탐색
정렬된 상태에 적용할 수 있다
삽입/삭제 되더라도 정렬 상태 유지해야 한다
삽입/삭제 빈번하면 부적합 할 수도

⌛ 시간복잡도
O(logn)
✨ 방법
배열의 가운데 원소 A와 찾고 싶은 값 X를 비교
1. A랑 X가 같으면 => 탐색 성공
2. 탐색 값(X)보다 가운데 원소(A)가 크면 => 왼쪽 부분 이진 탐색 반복(순환/재귀 호출)
3. 반대로, X보다 A가 작으면 => 오른쪽 부분 이진 탐색 반복
=> 반복 할 때마다 원소의 개수 1/2으로 감소
🤖 코드
// 반복형태 이진 탐색 JavaScript
function binarySearch(배열, 길이, 탐색값) {
let left = 0;
let right = 길이 - 1;
while(left <= right) {
const mid = Math.floor((left + right) / 2)
if (탐색값 === 배열[mid]) {
return mid;
} else if(탐색값 < 배열[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1; // 탐색 실패
}보면서 끄저인거라 코드에 오류 있으면 알려주세요
퀵 정렬
특정 원소 기준 배열을 두 개로 나누고
퀵 정렬을 계속 적용
⌛ 시간복잡도
O(n2)
랜덤 값 선택하고 처음 원소가 교환하고 정렬하면 최악의 경우가 거의 안나온다고 한다
피벗: 양쪽으로 나눌 때 기준이 되는 원소
보통 배열의 첫 번째 원소를 피벗으로 사용
=> 피벗이 제자리 잡도록 정렬하는 방식
피벗 중심으로
왼쪽 모든 원소는 피벗보다 작고,
오른쪽 모든 원소는 피벗보다 크다
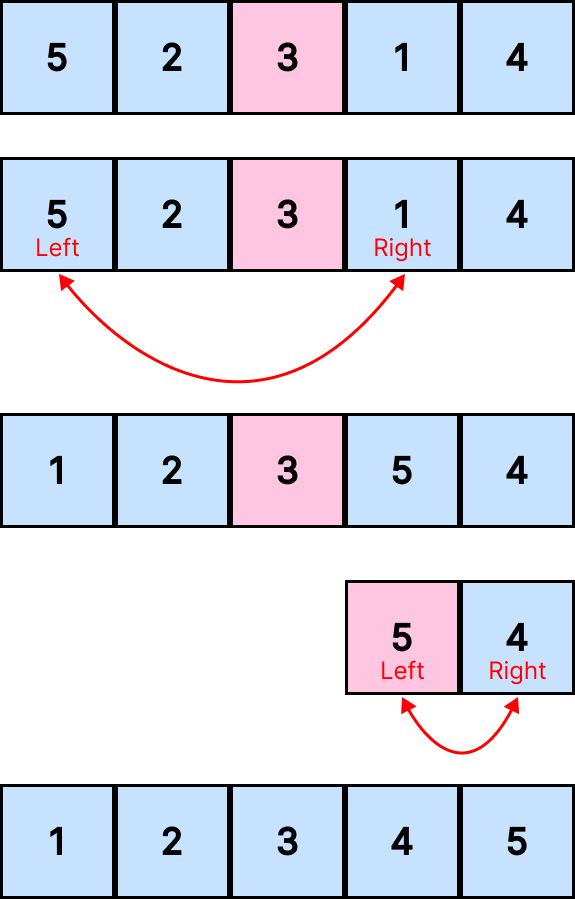
✨ 방법
분할: 피벗을 기준으로 두 부분으로 분할
정복: 나눈 부분에 대해 퀵 정렬 계속 적용(순환)하며 정렬
결합: X (위에서 다 정렬 하니끼 필요없다)
🤖 코드
// 퀵 정렬 JavaScript
function quickSort(배열, 길이){
if(길이 > 1){
피벗 = partition(배열[0.. 길이 - 1], 길이); // 두 부분으로 분할
quickSort(배열[0 .. 피벗-1], 피벗) // 왼쪽 부분 순환 호출
quickSort(배열[피벗+1 .. 길이-1], 길이 - 피벗 - 1) // 오른쪽 부분 순환 호출
}
}// partiton 함수
function partition(배열, 길이) {
let left = 1;
let rignt = 길이 - 1;
while(left < right) {
// 배열[0]은 피벗
while (left < n && 배열[left] < 배열[0]) {
left++
}
while (right > 0 && 배열[right] >= 배열[0]) {
right--
}
if(left < right) {
// 배열[left], 배열[right] 교환
// let temp = 배열[left]
// 배열[left] = 배열[right]
// 배열[right] = 배열[left]
// Destructure 방법으로 변경
[ 배열[left], 배열[right] ] =[ 배열[right], 배열[left] ]
} else {
// 피벗, 배열[right] 교환
// Destructure 방법으로 변경
// let temp = 배열[0] // 피벗
// 배열[0] = 배열[right]
// 배열[right] = 배열[0]
// Destructure 방법으로 변경
[ 배열[0], 배열[right] ] = [ 배열[right], 배열[0] ]
}
}
return right;
}
퀵 정렬 방법을 어떨 때 사용하는지
왜 사용하는지 이해를 더 해야겠다
아직 구조가 팍 오지 않는다
----------------
다시 읽어보고 시뮬레이션 돌려보니
이제 퀵정렬 움직임은 파악!!
'Computer Science > Algorithm :: 알고리즘' 카테고리의 다른 글
| 알고리즘 5강 :: 동적 프로그래밍 알고리즘 원리, 연쇄 행렬 곱셈 (0) | 2022.02.28 |
|---|---|
| 알고리즘 4강 :: 합병 정렬, 선택 문제 (0) | 2022.02.26 |
| 알고리즘 2강 :: 대표적인 알고리즘 3가지, 점근 성능 (0) | 2022.02.24 |
| 알고리즘 1강 :: 모든 자료구조 구현은 배열과 연결리스트 (0) | 2022.02.22 |
| 알고리즘 :: 그래프, 그래프 알고리즘, BFS, DFS (0) | 2022.01.19 |