알고리즘 6강을 보며 배운내용
5강에 이어 6강도 동적 프로그래밍!
동적 프로그래밍의 포인트는
- 문제를 작은 문제로 쪼개고,
- 작은 문제에 대한 점화식을 이용해서 값을 구하고 저장
- 저장된 값과 점화식을 반복해서 이용해서
- 마지막까지 가서 문제의 답을 구하는 것
BUT
점화식 구하는게 쉽지않다
그럼 어떻게 할까?
유명한 점화식
그러면 우선은 유명한 점화식 이해를 먼저 하자
유명 점화식이 아무래도 여러 문제에 적용되어 있을 것
자주 보고, 사용하며 제대로 이해하면
다른 문제에 조금씩 변형하면서 사용가능할 것 같다
스트링 편집 거리
X = x1x2 ... xn
Y = y1y2 ... ym
문자열 X를 Y로 변환하는데 필요한 편집 연산의 최소 비용 구하는 것
삽입, 삭제, 변경에 대한 최소 비용
X = SNOWY
Y = SUNNY
SNOWY를 SUNNY로 변경할 때 드는 최소화 비용을 => '편집 거리'라고 부른다
⌛ 시간 복잡도
O(nm)
🧮 점화식

이런 문제를 만난적이 있다
목적지까지 최소의 비용을 구하는 것이었다
그 때 2차원 배열을 이용해 지도를 그리고
그 안에서 최솟값을 이용해서 문제를 풀었다
아마도 다시 풀게되도 그럴 것 같다
위의 점화식을 이해하면
다음 문제 풀 때 비용만 바꿔서 사용할 수 있을 것 같다
SNOWY => SUNNY 편집 거리

모든 정점간의 최단 경로
임의의 두 정점 간의 최단 경로
=> 플로이드 알고리즘 이용
플로이드 알고리즘(Floyd)
가중치의 합이 음수인 사이클이 존재하지 않는다
⌛ 시간 복잡도
O(n3)
🧮 점화식


알고리즘

저울 문제
무게 M인 물체를 추를 이용해 저울로 달 수 있는지 확인하는 문제
추의 무게와 물체의 무게는 모두 정수이어야 한다
⌛ 시간 복잡도
O(nM)
🧮 점화식
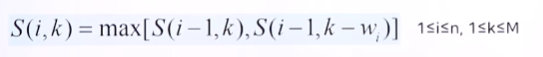
1번부터 i번까지 추를 이용해서, 무게 k인 물체 달 수 있는지에 대한 점화식
동적 프로그래밍 문제 예시
- 연쇄 행렬 곱셈(5강)
- 스트링 편집 거리(6강)
- 모든 정점간의 경로(6강)
- 저울 문제(6강)
'Computer Science > Algorithm :: 알고리즘' 카테고리의 다른 글
| 알고리즘 8강 :: 욕심쟁이, 최단경로, 작업스케쥴, 작업 선택 (0) | 2022.03.03 |
|---|---|
| 알고리즘 7강 :: 욕심쟁이, 동전거스름돈, 배낭문제, 신장트리 (0) | 2022.03.02 |
| 알고리즘 5강 :: 동적 프로그래밍 알고리즘 원리, 연쇄 행렬 곱셈 (0) | 2022.02.28 |
| 알고리즘 4강 :: 합병 정렬, 선택 문제 (0) | 2022.02.26 |
| 알고리즘 3강 :: 분할정복, 이진탐색, 퀵정렬 (0) | 2022.02.25 |