이산수학 마무리 하며 정리
✅ 이산수학에서 다루는 대상
- 이진 트리
✅ 알고리즘을 표현하는 방법
- 의사코드(Pseudocode)
- 순서도(flowchart)
- 컴퓨터 프로그래밍 언어
✅ 어떤 문제를 해결하기 위해 문제랑 관련 깊은 것만 남기도 다른 부분을 제거해서 명확하고 간단하게 만드는 것
- 추상화
✅ 명제
- 참과 거짓을 구별할 수 있는 문장이나 식
- ex) 명제: 지구에서는 육지가 바다 보다 넓다
- ex) 명제 아님: 2x - 6
✅ 모순 명제
- 항상 거짓의 값을 갖는 명제
- <--> 반대말: 항진 명제
✅ 유효 추론
- 주어진 참의 전제에 의해 유도된 결론이 참인 경우
✅ 허위 추론
- 주어진 참의 전제에 의해 유도된 결론이 거짓인 경우
✅ 특정한 공리를 가정하고, 그 가정 하에 제안된 명제가 참인 것을 입증하는 작업
- 증명
✅ 대우 증명법
- 'x2가 짝수면, x도 짝수'인 것을 증명할 때, 'x가 짝수가 아니면 x2'도 짝수가 아니다를 증명하는 것
- 앞뒤 뒤집고 부정해서 증명
✅ 모순 증명법
- 가설을 세우고, 증명을 해봐서 결과값이 참인지 확인하는 방법
✅ 전체 한정자
- 모든 값을 나타낸다
- ∀
- 전체 한정자에 대한 명제 함수를 만족시키려며 전체 값이 만족되어야 참
✅ 존재 한정자
- 논리 영역속 어떤 값을 나타낸다
- 어떤 하나만 가져도 참인 값을 갖는다
- ∃
✅ 서로소 집합
- 공통 원소가 없는 집합들
✅ 집합의 분할
- { { a, b }, { c } } 은 { a, b, c }의 분할
- 나눌 수 있는대로 다 나누는 것
- {a, b, c} 자체도 분할
- 겹치면 안된다 { { a, b }, { b, c } }는 { a, b, c }의 분할 아니다
✅ 멱집합(Power set)
- {a ,b}의 멱집합은 {Ø, {a}, {b}, {a, b}}
- 원소 개수는 2A
✅ 대칭차집합 ⊕
- 합집합에서 교집합 제외
- 안 겹치는 부분
- Exclusive Or
✅ 단위 행렬
- 대각 원소가 전부 1
- 다른 행렬에 단위 행렬 곱해도 변화 없다
✅ 대칭 행렬
- 주 대각선을 중심으로 대칭인 행렬
✅ 삼각행렬
- 상삼각행렬: 주대각선 밑으로 모두 0
- 하삼각행렬: 주대각선 위로 모두 0
✅ 부울행렬
- 모든 원소가 부울(0 또는 1)
✅ 행렬 곱
- ⊙
- A의 행의 개수와 B의 열의 개수가 같아야 된다
✅ 관계 R의 방향 그래프에서 순서쌍의 집합이란
- 각 원소가 가르키고 있는 원소를 하나씩 적으면 된다
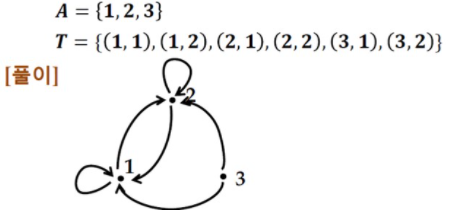
✅ 위의 순서쌍 집합(관계 R의 순서쌍 집합)을 부울행렬로 나타내기
- 각 자리에 1을 채워주면 된다
- 맨 왼쪽 위는 (1, 1)부터 시작

✅ 관계의 성질
- 반사적: 본인간의 관계 (1, 1), (2, 2) 같은 관계가 모든 원소에 있을 때
- 대칭적: (1, 2)가 있을 때, (2, 1)가 있으면 대칭적
- 추이적: (1, 2)가 있고, (2, 3)이 추이적이려면 (1, 3)이 있으면 된다
- 동치관계: 반사적 && 대칭적 && 추이적, 이렇게 전부되면 동치
✅ A={1, 2, 3}에서 B={a, b, c, d}로의 함수
- R = {(1, c), (2, b), (3, d)}
- 그럼 단사함수 같은거네?
✅ 전사함수
- X의 원소들이 Y의 원소 모두 가르키고 있을 때
- 겹쳐도 된다 그저 X모두가 사용되면 된다
✅ 단사함수
- X의 원소들이 Y의 원소 모두 가르키는건 전사함수랑 같은데
- 겹치면 안된다
✅ 전단사 함수
- X의 원소 개수와 Y의 원소 개수가 같을 때
- 역함수 존재
- 전사이자 단사함수
✅ 부울식
- +: 논리합
- · : 논리 곱
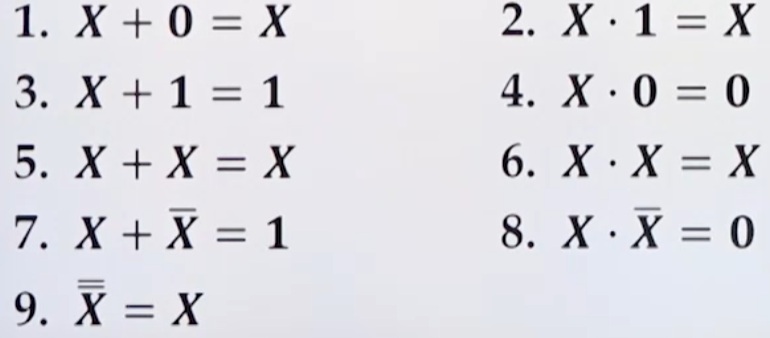
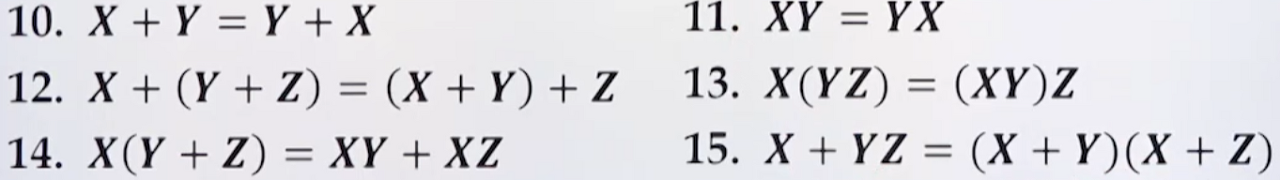
✅ 완전 그래프
- 꼭지점이 모든 꼭지점과 연결되 있는 그래프
✅ 이분 그래프
- 반 나눴을 때 같은 편끼리는 연결 안되어 있는데, 반대편이랑은 연결된 그래프

✅ 오일러 투어
- 모든 꼭지점의 차수가 짝수면 오일러 투어 만족
- 모든 변을 지나고 다시 시작점으로 돌아오면 오일러 투어
- 변 중심
✅ 해밀턴 사이클
- 모든 꼭지점을 한번만 지나서 시작점으로 돌아오면 해밀턴 사이클 만족
- 꼭지점 중심
✅ k-정규 그래프
- 모든 꼭지점이 동일한 수의 꼭지점과 연결
✅ 트리
- 연결 그래프로 사이클이 없어야 한다
- 트리의 차수는 한 트리 내의 각 노드 차수 중 최대값
- 트리의 무게는 리프 노드들의 전체 개수
- n개의 꼭지점을 가진 그래프가, n -1개의 변을 가지면 트리다
- 높이가 k인 완전 이진트리의 최대 노드 수는 2k+1 - 1이다
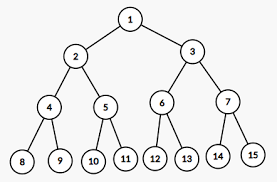
✅ 트리의 높이
- 루트 노드부터 마지막 자식 노드(리프 노드)까지 몇 번 가는지 세면된다
- 다음 트리 높이는 3
✅ 조합
- 순서가 관계없는 경우의 수
- C(n, r) = n! / r!(n - r)!
- 예시) x + y + z <= 5를 만족하는 경우의 수는?
신기하게도 C(5, 3)을 사용하면 된다
5! / 3!(5 - 3)! = 5! / 3!2! = 10
✅ 순열
- 순서를 고려해서 뽑는 경우의 수
- n개에서 r개를 뽑는 경우 P(n, r)
- n! / (n - r)!
- 중복 집합에서 순열은 n! / p! q! r!
- 예시) A에서 B로 가는 최단거리 방법 같은 것


'Computer Science > Discrete Mathematics :: 이산수학' 카테고리의 다른 글
| 이산수학 12강 :: 순열, 조합, 비둘기집의 원리 (0) | 2022.05.10 |
|---|---|
| 이산수학 11강 :: 트리, 이진트리, 완전이진트리, 이진탐색트리, 최소신장트리 (0) | 2022.05.03 |
| 이산수학 10강 :: 그래프(2/2), 평면 그래프, 오일러, 해밀턴, 가중 그래프, 최단 경로문제 (0) | 2022.04.26 |
| 이산수학 9강 :: 그래프(1/2), 용어, 종류 (0) | 2022.04.21 |
| 이산수학 8강 :: 디지털 논리회로, 부울대수, 부울대수 간소화 (0) | 2022.04.19 |