이산수학 11강 :: 트리, 이진트리, 완전이진트리, 이진탐색트리, 최소신장트리

이산수학 11강을 보며 배운내용

 

 

트리

사이클이 없는 단순 연결 그래프를 트리(tree)라고 한다

 

루트 트리

루트 노드로부터 서브 트리가 나와있다

 

트리 주요 용어

• 부모(parent) 노드
• 자식(child) 노드
• 형제(sibling) 노드
• 차수(degree): 자식 노드의 수

전체 차수는 트리 차수 중 가장 큰 것을 말한다

• 리프(leaf) / 단말(terminal) 노드: 자식이 없는 노드
• 레벨(level): 루트에서 N까지 경로의 길이
• 높이(height) / 깊이(depth) 
• 무게(weight): 리프 노드의 개수
• 닮은 트리: 트리의 구조는 동일하지만, 노드의 데이터가 다를 때

 

 

주요 정리
n개의 꼭지점을 갖는 트리는 n - 1개의 변을 가진다

 

 

이진 트리(Binary Tree)

공집합이거나,

모든 노드가 최대 2개의 서브트리를 갖는 루트 노드

 

루트 트리와 다른 점

1. 공집합을 가질 수 있다

2. 왼쪽과 오른쪽을 구분한다

 

최대 노드 수

이진 트리 T, 높이 h 일 때, T의 최대 노드 수

=> 2^h+1 - 1

 

 

완전 이진 트리

왼쪽 노드부터 채워진 이진 트리

jomuljomul.tistory.com/entry/%EC%99%84%EC%A0%84%EC%9D%B4%EC%A7%84%ED%8A%B8%EB%A6%ACComplete-Binary-Tree%EB%9E%80

 

n개의 노드를 갖는 이진트리의 최소 높이

자바스크립트 표현 => Math.floor(log₂n)

 

 

포화 이진 트리

모든 노드가 채워진 이진트리

sevity.tistory.com/141

 

 

이진 탐색 트리

이진 트리에서 모든 노드가 탐색을 위한 키(key)값을 가지고 있고,

다음 속성을 만족할 때

1. 왼쪽 서브트리의 값은 해당 루트 노드보다 작다
2. 오른쪽 서브트리의 값은 해당 루트 노드보다 크다

 

키 값에 대해 구성되는 트리가 달라진다

키 값 예시: A, B, C, D

 

이진 탐색 트리의 검색 방법

1. 탐색 노드를 루트 노드로 설정
   
   
2. 탐색 노드와 주어진 키를 비교
   
   
3. 일치하면 탐색 멈추고
   
   
4. 주어진 키가 현재 탐색 노드보다 작으면,
   왼쪽 자식을 탐색 노드로 설정, 왼쪽 자식 없으면 없음을 반환하고 탐색 중지
   
   
5. 키가 현재 탐색 노드보다 크면,
   오른쪽 탐색 노드로 설정, 오른쪽 자식 없으면 없음을 반환하고 탐색 중지

 

효율적인 이진 탐색 트리란?

• 비교 횟수가 적은 트리
• 비교 횟수 기댓값에 따라 구성
  : 검색 대상이 될 확률이 높은 것을 위에 두는 것

 

 

신장 트리(Spanning Tree) 조건?

• 그래프 G의 모든 꼭지점을 포함
• 사이클이 존재하지 않는 G의 부분 그래프

 

 

최소 신장 트리(MST: Minimum ST)

가중치의 합이 가장 작은 신장트리

blog.naver.com/PostView.nhn?blogId=ssarang8649&logNo=220992988177

 

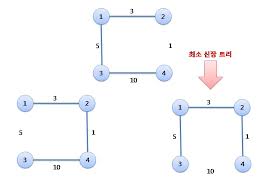
완전 그래프 K_n의 신장 트리 수는 n^n-2

 

 

MST 구하는 알고리즘

Kruskal 알고리즘

1. 가중치의 오름차순으로 변을 정렬
2. 가장 작은 가중치 변부터 트리에 추가
3. 사이클이 생기지 않게 모든 꼭지점이 포함되도록 계속 추가

 

Prim 알고리즘

1. 임의의 꼭지점 하나를 트리에 추가
2. 트리와 연결된 꼭지점 중에서 가장 작은 가중치 변으로 연결된 꼭지점 추가
3. 모든 꼭지점 연결될 때까지 방법 2번 반복

 

 

tree by Raychan @unsplash